Some
thirty years ago, Robert Leighton at Caltech developed a novel
photographic technique for measuring the Doppler velocity field
on the surface of the Sun and discovered, to his surprise, that
the velocity varied quasi-periodically on a time scale of five
minutes. However, the true nature of these oscillations, a superposition
of global coherent acoustic waves in which the entire Sun participates,
was not realized for about ten years. Since the early 1980's people
have been able to isolate individual eigenmodes of the Sun and
measure their frequencies accurately. These normal mode frequencies
have been used to investigate the internal structure and rotation
rate of the Sun.
Acoustic waves cannot propagate in a medium with variable density unless their wavelength is smaller than the length over which the density changes significantly. The rapid decrease in the density at the solar surface causes sound waves of frequency less than about 5mHz (periods greater than 3.3 minutes) to be reflected and thus trapped inside the Sun. Due to this trapping, the Sun rings at discrete frequencies which are its normal mode frequencies. In the Sun, several million of these normal modes are seen, with observed periods between 3 and 12 minutes, typical surface velocities of about 5 cm/s, and lifetimes of a few days. The individual normal modes of the Sun are identified by three numbers, analogous to the energy states of the hydrogen atom. These are the spherical harmonic degree l, azimuthal order m, and the number of nodes in the radial direction, n.
The observed l range for solar oscillations is 0 - 3000. The pattern of velocity at the surface for a mode of l = 12 and m = 10 is shown in figure 1. Because of the increase of sound speed with depth, non-radial inward propagating waves are refracted back toward the surface. Therefore, lower degree modes, corresponding to almost radial propagation, penetrate deeper in the Sun. For instance, modes of l = 0 have nonzero amplitude at the Solar center, whereas l = 50 modes are trapped in the outer 1/3 radius of the Sun. Thus the measurement of frequencies of different l and n modes enables us to determine the sound speed and other variables in the solar interior as a function of depth. These oscillations have provided a powerful observational tool in the study of the solar interior, in a way similar to the use of earthquakes by seismologists.
Figure 1. The velocity field at the solar surfaces associated iwth a mode of l=12 and m=10. Bright regions are moving toward us and dark regions are away; of course, this oscillates with time.
The observation that revealed the global nature of the Solar oscillations used the idea, mentioned above, that the frequencies of trapped coherent oscillations are the eigenfrequencies, which take on discrete values at any given wavenumber or l. The two dimensional power spectrum of oscillations, called l-n diagram (wave number vs. frequency diagram), was observed to contain discrete ridges; different ridges correspond to eigenmodes with different numbers of nodes in the radial direction. This established that these oscillations are superpositions of global, nonradial, acoustic normal modes (known as p-modes) of the Sun. The figure below shows a modern day version of this diagram.
With the recent significant improvements in observations, frequencies of normal modes in the Sun, with l up to 400, have been measured with an accuracy of about one part in 105.
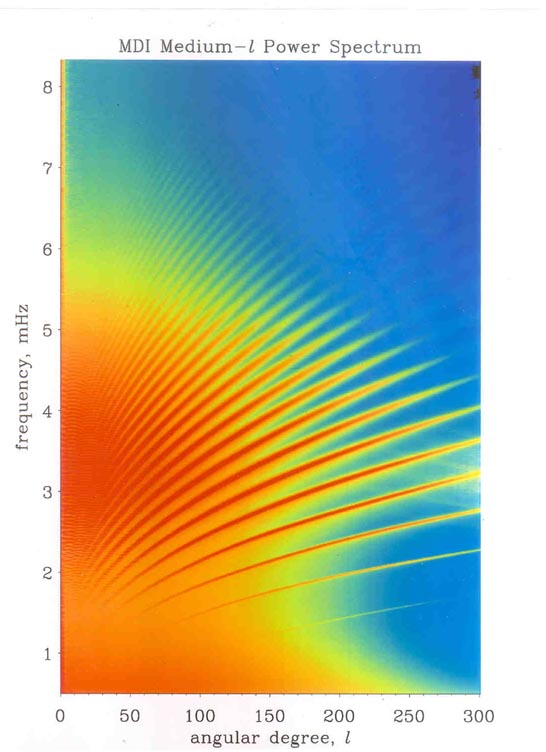
Figure
2. Power in solar oscillations as a function of horizontal wavenumber
(l,
)
and temporal frequency. For local pulsations the power would be
distributed smoothly in the plane. Different ridges in this diagram
correspond to normal mode oscillations with different number of
radial nomes n (n=1 for the lowest lying ridge;
from Soho/MDI).
These
observed frequencies have been used to determine the sound speed
as a function of the radial distance throughout most of the Solar
interior and is found to be in excellent agreement with the theoretical
expectations. (The error in temperature in theoretical solar models
is found to be less than 0.1% between the radius of 0.1 and 0.9Unfortunately, only the lowest degree p-modes
penetrate the energy producing core of the Sun, so we have limited
information about the solar core on the basis of helioseismological
analysis.
Another interesting discovery made using oscillations is the determination of the rotation profile in the solar interior. The basic idea here is very simple. The frequencies of modes of the same n and l and different m states are degenerate for any spherically symmetric system such as a non-rotating sun. Rotation lifts this degeneracy in a way that is analogous to the Zeeman splitting of energy states in atoms. Measurement of this rotational splitting for solar p-modes has enabled us to map the rotation of the Solar interior. It is found that most of the Sun is rotating at a speed which is not very different from the surface rate. The measured rotation profile implies that the quadrupole moment of the Sun, due to centrifugal distortion, is about 1.5 x 10-7.According to Newtonian gravity, a non-spherical Sun causes perihelion shift of planets. However, the measured quadrupole distortion of the Sun is too small to account for the 42.5 arc second per century perihelion advance of Mercury that is not explained otherwise by the Newtonian theory. This result lends support to Einstein's theory of general relativity and provides an additional constraint for non-standard theories of gravity.
The energy in the outer one third of the sun is transported by convection (fig.3). The convective motions, believed to be turbulent, generate sound waves; a familiar example of this process at work is the noise associated with the jet engine's tubulent exhaust. It is generally believed that the solar p-modes are excited due to acoustic waves emitted by the turbulent convection. The mathematical theory for sound generation by homogeneous turbulence was worked out in the 1950's and recently extended by Pawan Kumar, who, with Peter Goldreich of CalTech, applied it to the excitation of Solar p-modes (which is measured observationally by dividing mode energy by the decay time) due to this process is found to be in good agreement with the observations over the entire frequency range of 2-10mHz.
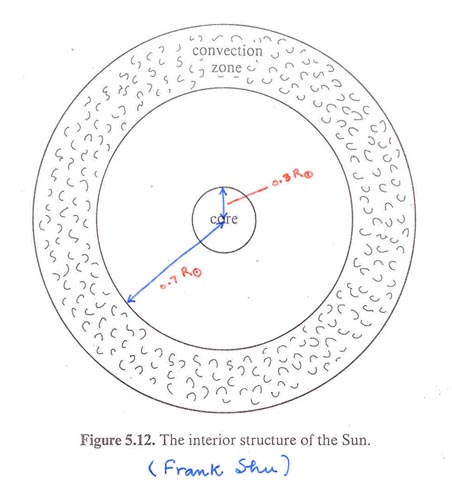
Figure 3. The interior structure of the Sun. Energy is produced in the core which is a region of size 25% of the solar radius. Energy is transported by photons in the interior (labeled radiation zone) and by convective motions in the outer part.
Acoustic waves of frequency greater than 5mHz are not trapped in the Sun, and yet the observed power spectra contain peaks out to at least 10mHz. According to Kumar, these peaks result from constructive interference of waves which meet at the surface, having followed different paths; one directly from the source to the surface and another traversing from the source downward through the solar interior and refracting upwards due to the increasing sound speed. The frequencies of peaks in the power spectrum in this case depend on the difference between the path length of these waves, which is sensitive to the depth of sources. By contrast, trapped p-mode frequencies are the eigenfrequencies of the Sun and do not depend on the location of sources. Using this method, Kumar finds that the acoustic emission in the Sun peaks about 100km below the observed surface, and the power spectrum of turbulence, perhaps surprisingly, is the same as that of homogeneous turbulence (Kolmogorov spectrum).
Helioseismology is continuing
to grow rapidly. There are two major observational efforts underway
to study Solar oscillations. One is a NSF funded ground-based
network of six telescopes, placed around the globe so as to reduce
the day/night gap in the observation of the Sun. This project,
named GONG (Global Oscillations Network Group), has been operating
since 1995 and has considerably improved the oscillation data
for modes of low degree (l < 200). The other observatory is
space based, funded jointly by NASA and the European space agency,
and launched in 1995. It observes the Sun outside the blurring
effect of Earth's atmosphere at high spatial resolution to enable
us to observe modes of very small horizontal wavelength or very
high degree (l 
3000). These observatories
have contributed much to our understanding of the structure and
dynamics of the interior of our nearest star.